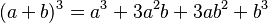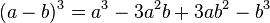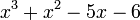http://www.eplc.umich.mx/salvadorgs/matematicas1/contenido/CapIII/3_9_1_fact_com.htm
Caso I - Factor común
Sacar el factor común es añadir la literal común de un
polinomio,
binomio o
trinomio,
con el menor exponente y el divisor común de sus coeficientes, y para
sacar esto, hay una regla muy sencilla que dice: Cuadrado del primer
término más o menos cuadrado del segundo por el primero más cuadrado del
segundo, y no hay que olvidar, que los dos que son positivos iguales
funcionan como el primer término, sabiendo esto, será sumamente sencillo
resolver los factores comunes.
Factor común monomio
Factor común por agrupación de términos

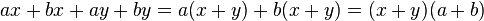 y si solo si el polinomio es 0 y el tetranomio nos da x.
y si solo si el polinomio es 0 y el tetranomio nos da x.
Factor común polinomio
Primero hay que determinar el factor común de los coeficientes junto
con el de las variables (la que tenga menor exponente). Se toma en
cuenta aquí que el factor común no solo cuenta con un término, sino con
dos.
un ejemplo:

Se aprecia claramente que se está repitiendo el polinomio
(x-y), entonces ese será el factor común. El otro factor será simplemente lo que queda del polinomio original, es decir:

La respuesta es:

En algunos casos se debe utilizar el número
1, por ejemplo:

Se puede utilizar como:

Entonces la respuesta es:

Caso II - Factor común por agrupación de términos
Para trabajar un polinomio por agrupación de términos, se debe tener
en cuenta que son dos características las que se repiten. Se identifica
porque es un número par de términos.
Un ejemplo numérico puede ser:

entonces puedes agruparlos de la siguiente manera:

Aplicamos el caso I (Factor común)


Caso III - Trinomio Cuadrado Perfecto
Se identifica por tener tres términos, de los cuales dos tienen
raíces cuadradas exactas, y el restante equivale al doble producto de
las raíces del primero por el segundo. Para solucionar un Trinomio
Cuadrado Perfecto debemos reordenar los términos dejando de primero y de
tercero los términos que tengan raíz cuadrada, luego extraemos la raíz
cuadrada del primer y tercer término y los escribimos en un paréntesis,
separándolos por el signo que acompaña al segundo término, al cerrar el
paréntesis elevamos todo el binomio al cuadrado.
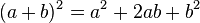
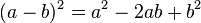
Ejemplo 1:

Ejemplo 2:

Ejemplo 3:

Ejemplo 4:

Organizando los términos tenemos

Extrayendo la raíz cuadrada del primer y último término y
agrupándolos en un paréntesis separados por el signo del segundo término
y elevando al cuadrado nos queda:

Al verificar que el doble producto del primero por el segundo término es
-20xy determinamos que es correcta la solución. De no ser así, esta solución no aplicaría.
Caso IV - Diferencia de cuadrados
Se identifica por tener dos términos elevados al cuadrado y unidos
por el signo menos. Se resuelve por medio de dos paréntesis, (parecido a
los productos de la forma (a-b)(a+b), uno negativo y otro positivo.

O en una forma más general para exponentes pares:

Y utilizando una productoria podemos definir una factorización para cualquier exponente, el resultado nos da r+1 factores.

Ejemplo 1:

Ejemplo 2: Supongamos cualquier r, r=2 para este ejemplo.

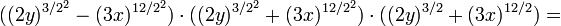

La factorización de la diferencia o resta de cuadrados consiste en
obtener las raíz cuadrada de cada término y representar estas como el
producto de binomios conjugados.
Caso V - Trinomio cuadrado perfecto por adición y sustracción
Se identifica por tener tres términos, dos de ellos son cuadrados
perfectos, pero el restante hay que completarlo mediante la suma para
que sea el doble producto de sus raíces , el valor que se suma es el
mismo que se resta para que el ejercicio original no cambie.

Nótese que los paréntesis en "(xy-xy)" están a modo de aclaración visual.
Caso VI - Trinomio de la forma x2 + bx + c
Se identifica por tener tres términos, hay una literal con exponente
al cuadrado y uno de ellos es el término independiente. Se resuelve por
medio de dos paréntesis, en los cuales se colocan la raíz cuadrada de la
variable, buscando dos números que multiplicados den como resultado el
término independiente y sumados (pudiendo ser números negativos) den
como resultado el término del medio.
Ejemplo:

Ejemplo:
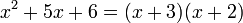
Caso VII - Suma o diferencia de potencias a la n
La suma de dos números a la potencia
n, a
n +b
n se descompone en dos factores (siempre que
n sea un número impar):
Quedando de la siguiente manera:

Ejemplo:

La diferencia también es factorizable y en este caso no importa si
n es par o impar. Quedando de la siguiente manera:

Ejemplo:
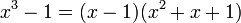
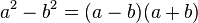
Las diferencias, ya sea de cuadrados o de cubos salen de un caso particular de esta generalización.
Caso VIII - Trinomio de la forma ax2 + bx + c
En este caso se tienen 3 términos: El primer término tiene un
coeficiente distinto de uno, la letra del segundo término tiene la mitad
del exponente del término anterior y el tercer término es un término
independiente, o sea sin una parte literal, así:

Para factorizar una expresión de esta forma, se multiplica el término independiente por el coeficiente del primer término(4x
2) :


Luego debemos encontrar dos números que multiplicados entre sí den
como resultado el término independiente y que su suma sea igual al
coeficiente del término x :


Después procedemos a colocar de forma completa el término x
2 sin ser elevado al cuadrado en paréntesis, además colocamos los 2 términos descubiertos anteriormente :
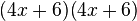
Para terminar dividimos estos términos por el coeficiente del término x
2 :

:

Queda así terminada la factorización :
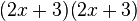
:

Caso IX - Cubo perfecto de Tetranomios
Teniendo en cuenta que los productos notables nos dicen que:
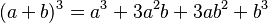
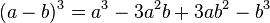
Caso X - Divisores binómicos
Su proceso consiste en los siguientes pasos.
Posibles ceros
En este primer paso los posibles ceros es el cociente de la división de los divisores del término independiente entre los divisores del coeficiente principal y se dividen uno por uno.
Nota: Para un mejor entendimiento, este método se explicara con el siguiente ejemplo.
Si el enunciado es este:
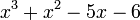
Se ve que el término independiente es 6 y el coeficiente principal es 1.
Para sacar los posibles ceros se procede de la siguiente manera:

Donde se puede notar que como se menciono anteriormente cada divisor de
arriba fue divido por el de abajo; es decir, que el uno se dividió entre
uno; el dos se dividió entre uno; el tres se dividió entre uno y por
último el seis se dividió entre uno.
http://es.wikiversity.org/wiki/Factorizaci%C3%B3n

 . En el proceso inverso, tenemos el producto 15 y se nos pide que lo factoricemos; entonces tendremos
. En el proceso inverso, tenemos el producto 15 y se nos pide que lo factoricemos; entonces tendremos 
 o
o  .
. y
y  no están factorizados por completo. Contienen factores que no son números primos. Los primeros números primos son 2, 3, 5, 7, 11, etc. Puesto que ninguna de esas factorizaciones está completa, notamos que en la primera factorización
no están factorizados por completo. Contienen factores que no son números primos. Los primeros números primos son 2, 3, 5, 7, 11, etc. Puesto que ninguna de esas factorizaciones está completa, notamos que en la primera factorización  , de modo que
, de modo que  mientras que la segunda factorización
mientras que la segunda factorización  , de modo que
, de modo que  , en cualquier caso la factorización completa para 20 es
, en cualquier caso la factorización completa para 20 es  .
. .
. 

 y si solo si el polinomio es 0 y el tetranomio nos da x.
y si solo si el polinomio es 0 y el tetranomio nos da x.









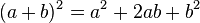
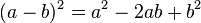











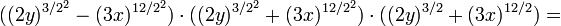



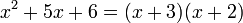



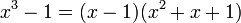
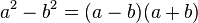





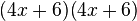
 :
:
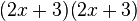 :
: